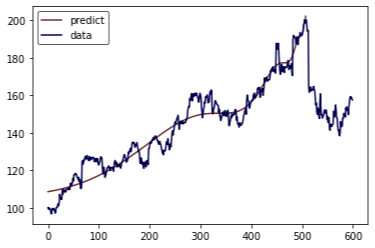
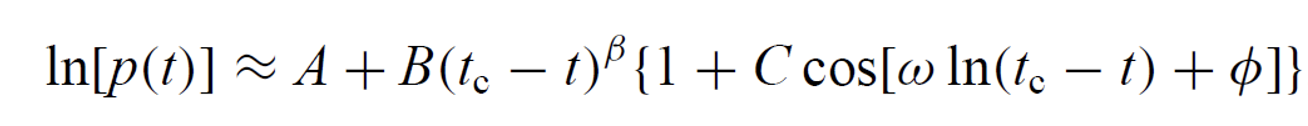Log-period power laws for bubble modeling

About this Project：

This is one of the assignment of (2021 Fall) Artificial Intelligence: Theory and Practice. We apply Genetic Algorithm to approximate the optimal solution by minimizing the average fitness error between time 0 and tc, in hope to detect the stock bubble in the field of finance.

這是 2021 Fall 所修陽明交大資財所開設【人工智慧理論與實務】的作業。將基因演算法(Genetic algorithm)應用在金融領域的股價泡沫，用真實數據解log-periodic power laws (LPPL) for bubble modeling的參數。

result1

The idea is to solve the parameters in two steps, first by obtaining the genes, which includes 4 non-linear variables tc, β, ω, Φ, with them plugged in to the function, we further use linear regression to estimate the optimal A, B, C. The fitness error is measured by Mean Absolute Error.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99

import numpy as np
import matplotlib.pyplot as plt
data = np.load('/AI/data.npy')

# Define Functions
def fitness(A,B,C,w,Beta,Phi,t_c,t):
    return (A + B*((t_c - t)**Beta)*(1+ C* np.cos(w*np.log(t_c - t)) + Phi))

def MAE(real, predict):
    """
    Mean absolute error
    as a measure of errors
    """
    return(np.mean(abs(real[:len(predict)]  - predict)))

def gene2coef(gene):
    w = ((np.sum(2**np.arange(10)*gene[0:10]))*3.15/1023)+4  
    Beta = ((np.sum(2**np.arange(10)*gene[10:20]))*0.4)/1023 + 0.25 
    Phi = (np.sum(2**np.arange(10)*gene[20:30]))*2*np.pi/1023
    t_c = np.rint(((np.sum(2**np.arange(10)*gene[30:40]))*15/1023)+500)
    return w, Beta, Phi, t_c

def gene(N,G,survive_rate,mutation_rate):

    mutation = round(N*40*mutation_rate)
    survive = round(N*survive_rate)
    pop = np.random.randint(0,2,(N,40)) # the first group of population
    fit =  np.zeros((N,1)) 

    for generation in range(G):
        for i in range(N):
            w, Beta, Phi, t_c = gene2coef(pop[i,:])
            t_c = int(t_c)
            M = np.zeros((t_c,3))
            for t in range(t_c):
                M[t,0] = 1
                M[t,1] = (t_c-t)**Beta
                M[t,2] = ((t_c-t)**Beta)*np.cos(w*np.log(t_c-t)+Phi)
            ABD = np.linalg.lstsq(M,ln_data[:t_c],rcond=None)[0]
            A,B,C = ABD[0], ABD[1], ABD[2]/ABD[1]
            predict = np.zeros(t_c)
            for t in range(t_c):
                predict[t] = np.exp(fitness(A,B,C,w,Beta,Phi,t_c,t))
            fit[i] = MAE(data,predict)
        
        sortf = np.argsort(fit[:,0]) 
        pop = pop[sortf,:] 

        for i in range(survive,N): #killing 
            fid = np.random.randint(0,survive) #0~99 Gene masking
            mid = np.random.randint(0,survive)
            while(fid==mid):
                mid = np.random.randint(0,survive)
            mask = np.random.randint(0,2,(1,40))
            son = pop[mid,:].copy()
            father = pop[fid,:]
            son[mask[0,:]==1] = father[mask[0,:]==1]
            pop[i,:] = son
        for i in range(mutation):
            m = np.random.randint(0,N)
            n = np.random.randint(0,40)
            pop[m,n] = 1-pop[m,n]

    for i in range(N):
        w, Beta, Phi, t_c = gene2coef(pop[i,:])
        t_c = int(t_c)
        M = np.zeros((t_c,3))
        for t in range(t_c):
            M[t,0] = 1
            M[t,1] = (t_c-t)**Beta
            M[t,2] = ((t_c-t)**Beta)*np.cos(w*np.log(t_c-t)+Phi)

        ABD = np.linalg.lstsq(M,ln_data[:t_c],rcond=None)[0]
        A,B,C = ABD[0], ABD[1], ABD[2]/ABD[1]
        predict = np.zeros(t_c)
        for t in range(t_c):
            predict[t] = np.exp(fitness(A,B,C,w,Beta,Phi,t_c,t))
        fit[i] = MAE(data,predict)
    sortf = np.argsort(fit[:,0]) 
    pop = pop[sortf,:]


    w, Beta, Phi, t_c = gene2coef(pop[0,:])
    t_c = int(t_c)
    M = np.zeros((t_c,3))
    for t in range(t_c):
        M[t,0] = 1
        M[t,1] = (t_c-t)**Beta
        M[t,2] = ((t_c-t)**Beta)*np.cos(w*np.log(t_c-t)+Phi)
    ABD = np.linalg.lstsq(M,ln_data[:t_c],rcond=None)[0]
    A,B,C = ABD[0], ABD[1], ABD[2]/ABD[1]
    predict = np.zeros(t_c)
    for t in range(t_c):
        predict[t] = np.exp(fitness(A,B,C,w,Beta,Phi,t_c,t))
    
    return A,B,C,w,Beta,Phi,t_c


1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17

# the main part
ln_data = np.log(data)
N,G,survive_rate,mutation_rate = 10000,30,0.05,0.001
A,B,C,w,Beta,Phi,t_c = gene(N,G,survive_rate,mutation_rate)
predict = np.zeros(int(t_c))
for t in range(t_c):
    predict[t] = np.exp(fitness(A,B,C,w,Beta,Phi,t_c,t))
print(np.mean(abs(data[:len(predict)]  - predict)))
x = np.arange(0,t_c)
x2 = np.arange(0,600)
plt.plot(x, predict, label = "predict")
plt.plot(x2, data[:], label = "data")
plt.legend()
plt.show()